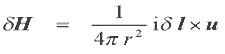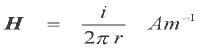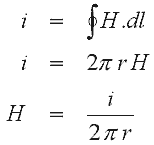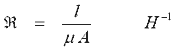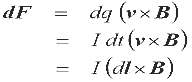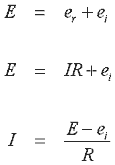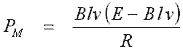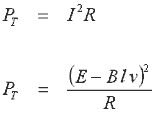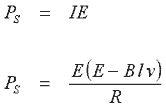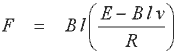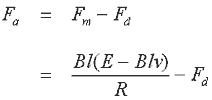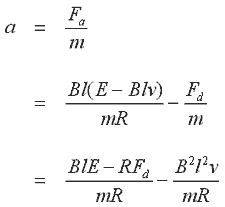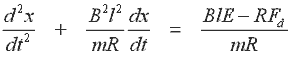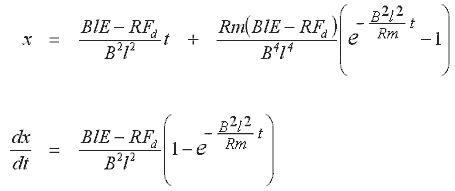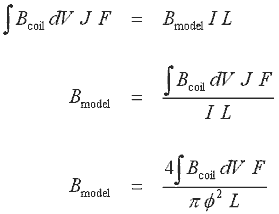Перевод статьи с http://www.coilgun.eclipse.co.uk/ by Roman.

 

Основы электромагнетизма

В этом разделе мы рассмотрим общие электромагнитные принципы, которые широко используются в инженерии. Это очень краткое введение в столь сложную тему. Вы должны найти себе хорошую книгу по магнетизму и электромагнетизму, если Вы хотите лучше понять этот раздел. Вы так же можете найти большинство из этих концепций детально изложенных в Fizzics Fizzle(http://library.thinkquest.org/16600/advanced/electricityandmagnetism.shtml).

Электромагнитные поля и силы

Перед тем, как мы будем рассматривать частный случай – coilgun-а, нам необходимо кратко ознакомиться с основами электромагнитных полей и сил. Всякий раз, когда существует движущийся заряд, существует соответствующее магнитное поле, ассоциированное с ним. Оно  может возникать из-за тока в проводнике, вращения электрона по своей орбите, потока плазмы и т.д. Для облегчения понимания электромагнетизма мы используем концепцию электромагнитного поля и магнитных полюсов. Дифференциальные векторные уравнения, которые описывают это поле, были разработаны James Clark Maxwell.

 1. Системы измерений

Только для того, чтобы усложнить жизнь, существуют три системы измерений, которые популярно используются. Они называются Sommerfield, Kennely и Gaussian. Так как каждая система имеет различные элементы (названия) для множества одинаковых вещей можно запутаться. Я буду использовать Sommerfield Систему, которая показана ниже:

Таблица 1. Sommerfield Система измерения

2. Закон Био-Савара

С помощью закона Био-Савара можно определить магнитное поле, создаваемое элементарным током.

Рис 2.1

 

 

где  H компонента поля на расстоянии r, созданная током i, текущим в элементарном участке проводника длиной l . u единичный вектор направленный радиально от l.

Мы можем определить магнитное поле, создаваемое сочетанием нескольких элементарных токов используя этот закон. Рассмотрим бесконечно длинный проводник, по которому течет ток i. Мы можем использовать закон Био-Савара для получения основного решения для поля на любой дистанции от проводника. Я не буду приводить получение этого решения здесь, любая книга по электромагнетизму детально покажет это. Основное решение: 

 

 

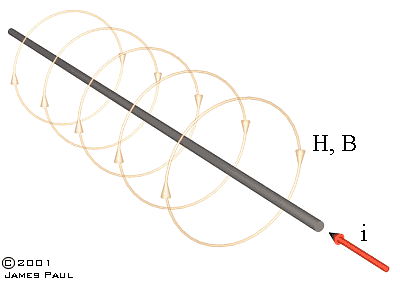
Рис 2.2

 

Поле по отношению к проводнику с током циклическое и концентрическое.

(Направление магнитных линий (векторов H, B) определяется по правилу буравчика (штопора). Если поступательное движение буравчика соответствует направлению тока в проводнике, то вращательное направление рукоятки укажет направление векторов.)

Другой случай, который имеет аналитическое решение – это осевое поле витка с током. Пока мы можем получить аналитическое решение для осевого поля, но это невозможно сделать для поля в целом. Для нахождения поля в какой-то произвольной точке нам необходимо решить комплексные интегральные уравнения, что лучше всего сделать с помощью цифровых методов.

 3. Закон Ампера

Это альтернативный метод определения магнитного поля, использует группу проводников проводящих ток. Закон может быть записан как:

где N номер проводника несущего ток i и l линейный вектор. Интегрирование должно сформировать закрытую линию вокруг проводника с током. Рассматривая бесконечный проводник с током, мы снова можем применить закон Ампера, как показано ниже:

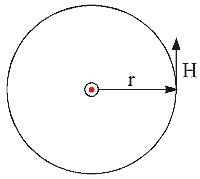
Рис 3.1

Мы знаем, что поле циклическое и концентрическое вокруг проводника с током, поэтому H может быть проинтегрировано по кольцу (вокруг проводника с током) на дистанции r, что дает нам: 

Интегрирование очень простое и показывает, как закон Ампера может быть применен для получения быстрого решения в некоторых случаях (конфигурациях). Знание структуры поля необходимо перед тем, как этот закон может быть применен.

(Поле (напряженность) в центре кругового поля (витка с током) )

 4. Поле соленоида

Когда заряд движется в катушке, он создает магнитное поле, направление которого может быть определено при помощи правила правой руки (возьмите Вашу правую руку, согните пальцы в направлении тока, отогните большой палец, направление, указываемое большим пальцем, показывает на магнитный север вашей катушки). Соглашение для магнитного потока говорит, что магнитный поток начинается из северного полюса и заканчивается на южном. (The convention for the direction of flux has the flux emerging from a north pole and terminating on a south pole). Линии поля и магнитного потока представляют собой закрытые витки вокруг катушки. Запомните, что этих линий на самом деле нет, они просто соединяют точки равного значения. Это слегка напоминает контуры на карте, где линии показывают точки одинаковой высоты. Высота земли непрерывно изменяется между этими контурами. Так же поле и магнитный поток непрерывны (изменение не обязательно плавное – дискретное изменение в проницаемости  вызывает острое изменение значения поля, немного похоже на скалы на карте).

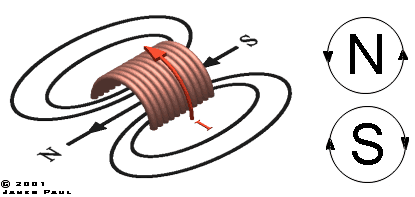
Рис 4.1

Если соленоид длинный и тонкий, то поле внутри соленоида может считаться почти однородным.

5. Ферромагнитные материалы

Возможно, наиболее хорошо известный ферромагнитный материал – железо, но есть и другие элементы, такие как кобальт и никель, а так же многочисленные сплавы, как кремниевая сталь. Каждый материал имеет особое свойство, которое делает его пригодным для его применения. Итак, что мы подразумеваем под ферромагнитным материалом? Это просто, ферромагнитный материал притягивается магнитом. Несмотря на то, что это так, это едва ли полезное определение, и оно не говорит нам, почему происходит притяжение. Подробная теория магнетизма материалов очень сложная тема, включающая квантовую механику, поэтому мы будем придерживаться простого концептуального описания. Как Вам известно, поток зарядов создает магнитное поле, поэтому, когда мы обнаруживаем движение заряда, мы должны ожидать ассоциированного с ним магнитного поля. В ферромагнитных материалах орбиты электронов распределены в таком порядке, что происходит создание небольшого магнитного поля. Тогда это значит, что материал состоит из множества мельчайших витков с током, которые имеют свои собственные магнитные поля. Обычно, витки, ориентированные в одну сторону, объединяются в маленькие группы, называемые доменами. Домены направлены в произвольном направлении в материале, поэтому в материале нет общего магнитного поля (результирующее поле равно нулю). Тем не менее, если мы приложим внешнее поле к ферромагнитному материалу от катушки или постоянного магнита, виточки с токами развернуться по направлению с этим полем. (However if we apply an external field to the ferromagnetic material from a coil or permanent magnet, the current loops try and align with this field - the domians which are most aligned with the field 'grow' at the expense of the less well aligned domains). Когда это случится, результатом будет намагничивание и притяжение между материалом и магнитом/катушкой.

6. Магнитная индукция и проницаемость

Получение магнитного поля имеет ассоциированную с ним плотность магнитного потока, так же известную как магнитная индукция. Индукция B соединена с полем через проницаемость среды, через которую поле распространяется. 

где 0 проницаемость в вакууме и r относительная проницаемость. Индукция измеряется в теслах (Тл). 

(Интенсивность магнитного поля зависит от среды, в которой оно возникает. Сравнивая магнитное поле в проводе, расположенном в данной среде и в вакууме, установили, что в зависимости от свойств среды (материала) поле получается более сильным, чем вакууме (парамагнитные материалы или среды), или, наоборот, более слабым (диамагнитные материалы и среды). Магнитные свойства среды характеризуются абсолютной магнитной проницаемостью μ_а.

Абсолютная магнитная проницаемость вакуума называется магнитной постоянной μ₀. Абсолютную магнитную проницаемость различных веществ (сред) сравнивают с магнитной постоянной (магнитной проницаемость вакуума).Отношение абсолютной магнитной проницаемости какого-либо вещества к магнитной постоянной называют магнитной проницаемостью (или относительной магнитной проницаемостью), так что

Относительна магнитная проницаемость – отвлеченной число. Для диамагнитных веществ μ_r < 1, например для меди μ_r = 0,999995. Для парамагнитных веществ μ_r > 1, например для воздуха μ_r = 1,0000031.При технических расчетах относительная магнитная проницаемость диамагнитных и парамагнитных веществ принимается равной 1.

У ферромагнитных материалов, играющих исключительно важную роль в электротехнике, магнитная проницаемость имеет разные значения в зависимости от свойств материала, величины магнитного поля, температуры и достигают значений десятков тысяч.)

7. Намагничивание

Намагничивание материала – это мера его магнитной ‘силы’. Намагничивание может быть присуще материалу, такому как постоянный магнит или оно может быть вызвано внешним источником магнитного поля, к примеру, соленоидом. Магнитная индукция в материале может быть выражена как сумма векторов намагничивания M и магнитного поля H.

 

(Электроны в атомах, двигаясь по замкнутым орбитам или элементарным контурам вокруг ядра атома, образуют элементарные токи или магнитные диполи. Магнитный диполь можно характеризовать вектором – магнитным моментом диполя или элементарного  электрического тока m, величина которого равна произведению элементарного тока i и элементарной площадки S, рис.8д.0.1, ограниченной элементарным клнтуром.

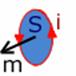
Рис. 8д.0.1

 

Вектор m направлен перпендикулярно площадке S;, направление его определяется по правилу буравчика. Векторная величина, равная геометрической сумме магнитных моментов всех элементарных молекулярных токов в рассматриваемом теле (объеме вещества), представляет собой магнитный момент тела

Векторная величина, определяемая отношением магнитного момента M’ к объему V, называется средней намагниченностью тела или средней интенсивностью намагничивания

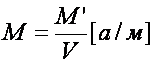
Если ферромагнетик не находится во внешнем магнитном поле, то магнитные моменты отдельных доменов направлены самым различным образом, так что суммарный магнитный момент тела оказывается равным нулю, т.е. ферромагнетик не намагничен. Внесение ферромагнетика во внешнее магнитное поле вызывает: 1-поворот магнитных доменов в направлении внешнего поля – процесс ориентации; 2-рост размеров тех доменов, направления моментов которых близки к направлению поля, и уменьшение доменов с противоположно направленными магнитными моментами – процесс смещения границ доменов. В результате ферромагнетик намагничивается. Если при увеличении внешнего магнитного поля все спонтанно намагниченные участки будут ориентированы в направлении внешнего поля и прекратится рост доменов, то наступит состояние предельной намагниченности ферромагнетика, называемое магнитным насыщением.

При напряженности поля Н магнитная индукция в неферромагнитной среде (μ_r = 1) была бы равна B₀=μ₀H. В ферромагнитной среде к этой индукции прибавляется индукция добавочного магнитного поля B_д= μ₀M.Результирующая магнитная индукция в ферромагнитном материале B=B₀+B_д=μ₀(H+M).)

8. Магнитодвижущая сила (МДС)

Это аналог электродвижущей силы (ЭДС) и она используется в магнитных схемах для определения плотности магнитного потока в разных направлениях цепи. МДС измеряется в ампер-витках или просто в амперах. Магнитная цепь эквивалентна сопротивлению и называется магнитным сопротивлением, которое определяется как

 

где l длина пути цепи,  проницаемость и A площадь поперечного сечения.

Давайте взглянем на простую магнитную цепь:

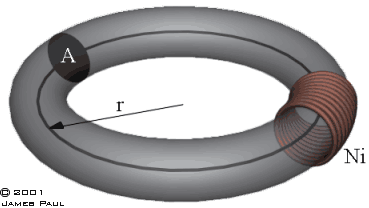
Рис. 8.1

Тор имеет средний радиус r и площадь поперечного сечения A. МДС генерируется катушкой с N витками, в которых течет ток i. Расчет магнитного сопротивления усложнен нелинейностями в проницаемости материала. 

Если магнитное сопротивление будет определено, тогда мы можем посчитать магнитный поток, который присутствует в цепи.

9. Размагничивающие поля

Если кусок ферромагнитного материала, по форме бруска, намагнитить, то на концах его появятся полюса. Эти полюса генерируют внутренне поле, которое пытается размагнитить материал – оно действует в обратном направлении полю, создающему намагниченность. В результате внутреннее поле будет намного меньше чем внешнее. Форма материала имеет большое значение на размагничивающее поле, длинный тонкий стержень (большое отношение длина/диаметр) имеет маленькое размагничивающее поле по сравнению, скажем, с широкой формой – как сфера. В перспективе разработки coilgun это значит, что снаряд с маленьким соотношением длина/диаметр требует более сильного внешнего поля, для достижения определенного состояния намагничивания. Взгляните на график ниже. Он показывает результирующее внутреннее поле вдоль оси двух снарядов – одного 20 мм длиной и 10 мм диаметре и другого 10 мм в длину и 20 мм в диаметре. Для одного и того же внешнего поля мы видим большую разницу во внутренних полях, более короткий снаряд имеет пик около 40% от пика длинного снаряда. Это очень удачный результат, показывающий разницу между разными формами снарядов. 

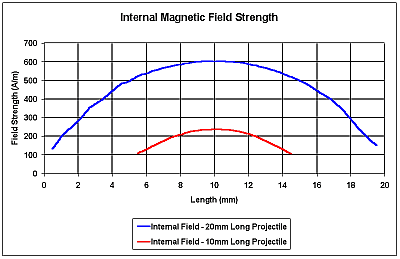
Рис. 9.1

 Следует отметить, что полюса формируются только там, где есть непрерывная проницаемость материала. На закрытом магнитном пути, как тор, полюса не возникают, и там нет размагничивающего поля.

10. Сила, действующая на заряженную частицу

Итак, как нам посчитать силу, действующую на проводник с током? Давайте начнем с рассмотрения силы, действующей на движущийся в магнитном поле заряд. (I'll adopt the general approach in 3 dimensions).

Эта сила определяется пересечением векторов скорости v и магнитной индукции B, и она пропорциональна величине заряда. Рассмотрим заряд q = -1.6x10^-19 К, движущийся со скоростью 500м/с в магнитном поле индукцией 0.1Tл, как показано ниже.

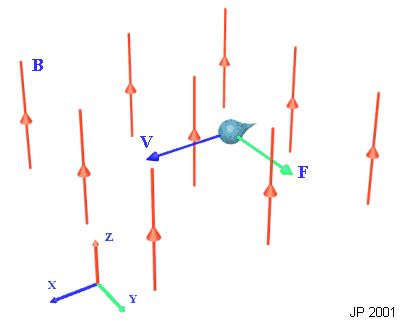
Рис. 10.1. Воздействие силы на движущийся заряд

Испытываемая зарядом сила, может быть просто вычислена, как показано ниже:

Вектор скорости 500 i м/с и индукция 0.1 k T, итак имеем:

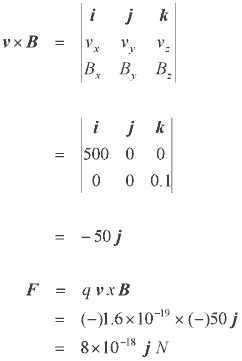
Очевидно, если ничего не будет противостоять этой силе, частица будет отклоняться (она должна будет описывать окружность в плоскости x-y для случая выше). Есть много интересных частных случаев, которые могут быть получены со свободными зарядами и магнитными полями – Вы прочли только об одном из них.

11. Сила, действующая на проводник с током

Теперь давайте отнесем то, что узнали к силе, действующее на проводник с током. Есть два различных пути для получения соотношения.

Мы можем описать условный ток, как показатель изменения заряда 

Теперь мы можем продифференцировать уравнение силы, данное выше, чтобы получить 

Комбинируем эти уравнения, получим

dl – вектор, показывающий направление условного тока. Выражение может быть использовано для анализа физической организации, например двигателя постоянного тока. Если проводник прямой, тогда это может быть упрощено до 

Направление действия силы всегда создает прямой угол к магнитному потоку и направлению тока. Когда используется упрощенная форма, направление силы определяется по правилу правой руки.

12. Индуцированное напряжение, закон Фарадея, закон Ленца

Последнее, что нам надо рассмотреть – это индуцированное напряжение. Это просто расширенный анализ воздействия силы на заряженную частицу. Если мы возьмем проводник (что-нибудь с мобильным зарядом) и придадим ему какую-то скорость V, относительно магнитного поля, на свободные заряды будет действовать сила, которая толкает их в один из концов проводника. В металлическом бруске будет разделение зарядов, где электроны будут собраны на одном из концов бруска. Рисунок ниже показывает общую идею.

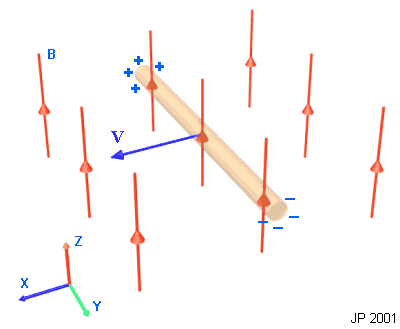
Рис. 12.1 Индуцированное напряжение при поперечном перемещении проводящего бруска

Результатом любого относительного движения между проводником и индукцией магнитного поля будет индуцированное напряжение, сгенерированное движением зарядов. Тем не менее, если проводник перемещается параллельно магнитному потоку (по оси Z в рисунке выше), тогда напряжение не будет индуцироваться.

Мы можем рассмотреть другую ситуацию, где открытая планарная поверхность пронизана магнитным током. Если мы поместим туда замкнутый контур C, тогда любое изменение в магнитном потоке, связанным с C будет порождать напряжение вокруг C.

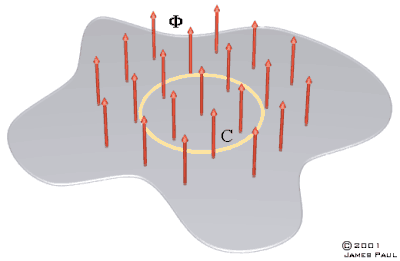
Рис. 12.2 Магнитный поток, связанный контуром 

Теперь, если мы представим проводник в виде замкнутого витка на месте C, тогда изменение магнитного потока будет индуцировать напряжение в этом проводнике, которое будет двигать ток по кругу в этом витке. Направление тока может быть определено, применив закон Ленца, который, попросту говоря, показывает, что результат воздействия направлен противоположно самому воздействию. В этом случае индуцированное напряжение будет двигать ток, который будет препятствовать изменению магнитного потока – если магнитный поток уменьшается, тогда ток будет пытаться поддержать магнитный поток неизменным (против часовой стрелки), если магнитный поток растет, тогда ток будет препятствовать этому увеличению (по часовой стрелке) (направление определено по правилу буравчика). Закон Фарадея устанавливает соотношение между индуцированным напряжением, изменением магнитного потока и временем: 

Минус учитывает закон Ленца.

 13. Индуктивность

Индуктивность может быть описана как отношение связанного магнитного потока к току, который этот магнитный поток создает. Для примера рассмотрим виток провода с площадью поперечного сечения A, в котором течет I.

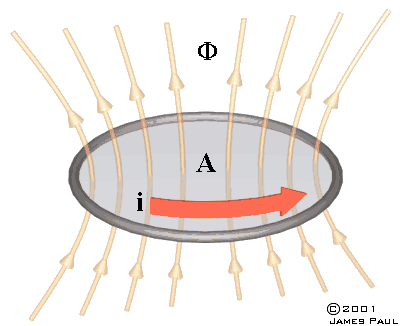
Рис. 13.1

Сама индуктивность может быть определена как

Если есть более одного витка, тогда выражение становиться

где N –кол-во витков.

Важно понять, что индуктивность – это только константа, если виток окружен воздухом. Когда появляется ферромагнитный материал, как часть магнитной схемы, тогда появляется нелинейное поведение системы, которое дает переменную индуктивность.

14. Преобразование электромеханической энергии

Принципы преобразования электромеханической энергии применимы ко всем электрическим машинам и coilgun не исключение. Перед рассмотрением coilgun давайте представим простой линейный электрический ‘мотор’, состоящий из поля статора и якоря, помещенного в это поле. Это показано на рис. 14.1. Заметьте, что в этом упрощенном анализе источник напряжения и ток якоря не имеют индуктивности, ассоциированной с ними. Это означает, что только индуцированное напряжение в системе является следствием движения якоря по отношению к магнитной индукции.

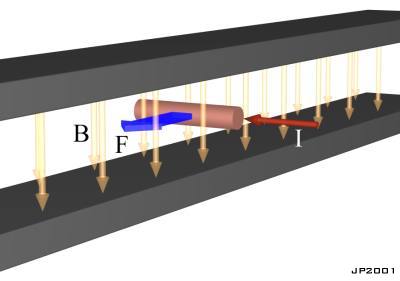
Рис. 14.1. Примитивный линейный мотор

Когда напряжение приложено к концам якоря, ток будет определяться в соответствии с его сопротивлением. Этот ток будет испытывать силу (I x B), заставляющую якорь ускоряться. Теперь, используя ранее рассмотренную секцию (12 Индуцированное напряжение, закон Фарадея, закон Ленца), мы показали факт того, что напряжение индуцируется в проводнике, перемещающемся в магнитном поле. Это индуцированное напряжение действует противоположно приложенному напряжению (по закону Ленца). Рис. 14.2 показывает эквивалентную схему, в которой электрическая энергия превращается в тепловую энергию P_T, и механическую энергию P_M.

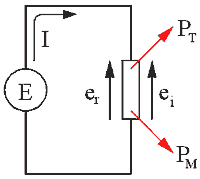
Рис. 14.2. Эквивалентная схема мотора

Теперь нам необходимо рассмотреть, как механическая энергия якоря относится к электрической энергии, передаваемой в него. Так как якорь расположен под прямым углом к полю магнитной индукции, сила определяется по упрощенному выражению 11.4

 так как мгновенная механическая энергия продукт силы и скорости, имеем 

где v – скорость якоря. Если мы применим закон Кирхгоффа к замкнутой цепи, мы получим следующие выражения для тока I.

Теперь, индуцированное напряжение может быть выражено как функция от скорости якоря 

Подставляя выр.14.4 в 14.3 получаем

и подставляя выр.14.5 в 14.2 получаем

Теперь давайте рассмотрим тепловую энергию, выделяющуюся в якоре. Она определяется по выр.14.7

И, наконец, мы можем выразить энергию, поставляемую в якорь как 

Заметьте так же, что механическая энергия (выр.14.2) – эквивалент тока I, умноженного на индуцированное напряжение (выр.14.4).

Мы можем построить эти кривые для того, чтобы увидеть, как поставляемая в якорь энергия сочетается с диапазоном скоростей. (We can plot these curves to show how the power supplied to the armature is distributed over a range of speeds). Чтобы этот анализ имел некоторое отношение к coilgun, мы дадим нашим переменным значения, которые соответствуют ускорителю coilgun. Начнем с плотности тока в проводе, из которого мы определим значения остальных параметров. Максимальная плотность тока, при тестировании была 90A/мм², итак если мы выберем длину и диаметр провода как

 

l = 10 m

D = 1.5x10^-3 m

 

тогда сопротивление провода и ток будут

 

R = 0.1

I = 160 A

 

Теперь у нас есть значения для сопротивления и тока, мы можем определить напряжение

 

V = 16 V

Все эти параметры необходимы для построения статических характеристик мотора. 

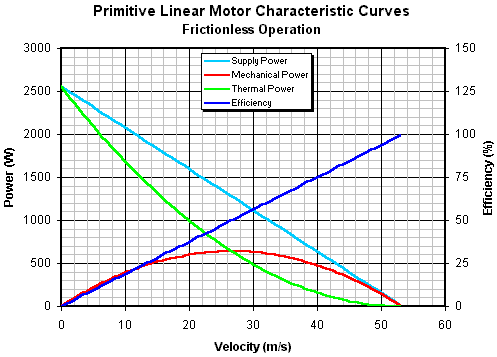
Рис. 14.3 Кривые характеристик для модели мотора без трения

Мы можем сделать эту модель немного более реалистичной, добавив силу трения, скажем, 2Н, так что уменьшение механической энергии будет пропорционально скорости якоря. Значение этого трения умышлено взято больше для того, чтобы эффект от этого был более очевиден. Новый набор кривых показан на рис.14.4.

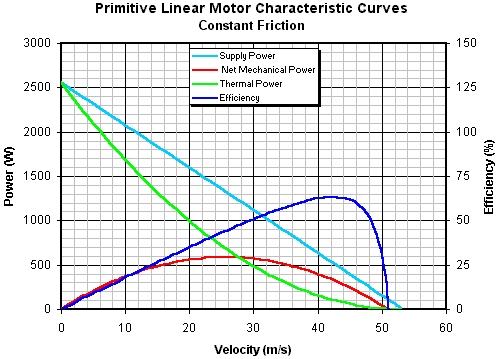
Рис. 14.4. Кривые характеристик с постоянным трением

Присутствие трения немного изменяет кривые энергий, так что максимальная скорость якоря немного меньше, чем в случае с нулевым трением. Наиболее заметная разница – это изменение кривой эффективности, которая теперь имеет пик и после него резко спадает, когда якорь достигает 'no-load' скорости. Эта форма кривой эффективности типична для мотора постоянного тока с постоянным магнитом.

Так же заслуживает рассмотрения то, как сила и, следовательно, ускорение зависят от скорости. Если мы подставим выр.14.5 в выр.14.1 мы получим выражение для F с точки зрения скорости v.

Построив эту зависимость, мы получим следующий график 

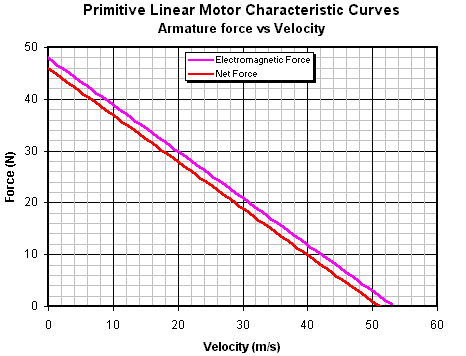
Рис. 14.5. Зависимость силы, действующей на якорь, от скорости

Ясно, что якорь стартует с максимально разгоняющей силой, которая начинает уменьшаться, как только якорь начинает двигаться. Хотя эти характеристики дают мгновенные  значения действующих параметров для определенной скорости, они должны быть полезны для того, чтобы увидеть, как ведет себя мотор во времени, т.е. динамически.

Динамическая ответная реакция мотора может быть определена решением дифференциального уравнения, которое описывает его поведение. Рис. 14.6 показывает диаграмму воздействия сил на якорь, по которой можно определить результирующую силу, описанную дифференциальным уравнением.

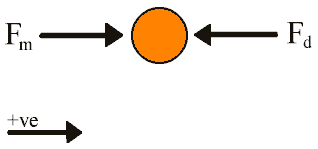
Рис. 14.6 Диаграмма воздействия сил на якорь

F_m и F_d – магнитная и противодействующая силы соответственно. Так как напряжение является постоянной величиной, мы можем использовать выр.14.1 и результирующая сила F_a, действующая на якорь, будет

Теперь мы можем записать выражение для ускорения якоря

Если мы запишем ускорение и скорость как производные от перемещения x относительно времени и перестроим выражение, мы получим дифференциальное уравнение для движения якоря

Это неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и оно может быть решено, определив дополнительную функцию и частный интеграл. Метод решения прямой (все программы математических университетов рассматривают дифференциальные уравнения), поэтому я просто приведу результат. Одно замечание – это частное решение использует начальные условия: x = 0, dx/dt = 0.

Нам необходимо назначить значение силе трения, магнитной индукции и массе якоря. Выберем трение. Я буду использовать значение 2Н для иллюстрирования, как оно изменяет динамические характеристики мотора. Определение значения индукции, которая будет создавать такую же ускоряющую силу в модели, как она делает это в тестовой катушке для данной плотности тока, требует, чтобы мы рассмотрели радиальную составляющую распределения плотности магнитного потока, созданного намагниченным снарядом coilgun (эта радиальная составляющая создает осевую силу). Для этого необходимо произвести интегрирование выражения, полученного умножением текущей плотности J и фактором заполнения F по объему, занятому катушкой. Выражение, затем, приравнивается BIL для нашей модели, и получаем B_model решением уравнения 14.15, где диаметр провода.

Мы можем рассмотреть магнитный поток, созданный намагниченным снарядом (без тока в катушке) как показано на рис. 14.7.

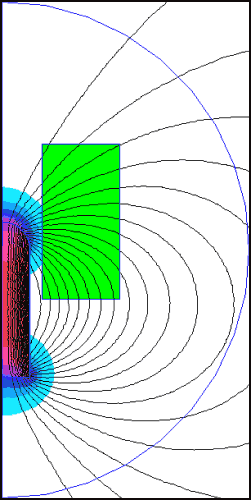
Рис. 14.7. Определение интеграла объема плотности радиального магнитного потока используя FEMM

Снаряд становится намагниченным, когда мы определим для него B-H кривую и Hc значения в FEMM диалоге свойств материала. Значения были выбраны для строгого соответствия с намагниченным железом. FEMM дает значение 6.74x10^-7 Tm³ для интеграла объема плотности магнитного потока B_coil, итак используя F = /4 мы получаем B_model = 3.0x10^-2 Tл. Это значение плотности магнитного потока может показаться очень маленьким, рассматривая плотность магнитного потока внутри снаряда, которая равна где-то 1.2Tл, однако, мы должны понять, что магнитный поток разворачивается в намного большем объеме вокруг снаряда только с частью магнитного потока, показанной в радиальной составляющей. Теперь Вы понимаете, что, согласно нашей модели, coilgun – это 'inside out'(вывернутый наизнанку) и 'back to front', другими словами в coilgun неподвижная медь окружает намагниченную часть, которая движется. Это не создает никаких проблем. Так сущность системы – это связанные линейная сила, действующая на статор, и якорь, поэтому мы можем зафиксировать медную часть и разрешить полю статора создавать движение. Генератор поля статора – это наш снаряд, назначим ему массу 12г.

Теперь мы можем изобразить перемещение и скорость как функции времени, как показано на рис. 14.8

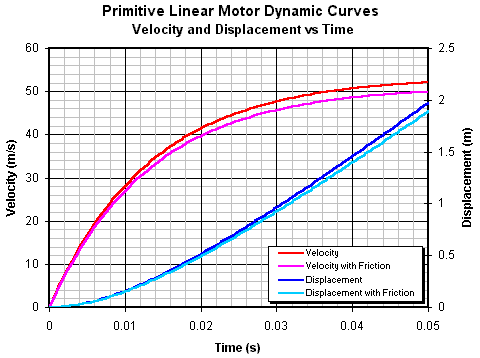
Рис. 14.8. Динамическое поведение линейного мотора

Мы также можем скомбинировать выражения скорости и перемещения для получения функции скорости от перемещения, как показано на рис. 14.9.

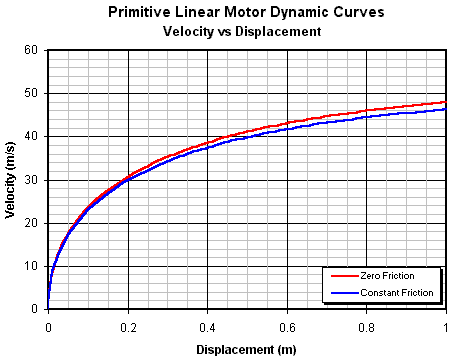
Рис. 14.9. Характеристика зависимости скорости от перемещения

Здесь важно отметить, что необходим относительно длинный акселератор, чтобы якорь начал достигать своей максимальной скорости. Это имеет смысл для построения максимально  эффективного практического ускорителя.

Если мы увеличим кривые, мы сможем определить, какая скорость будет достигнута на расстоянии равном длине активного материала в катушке пистолета-ускорителя (78 мм).

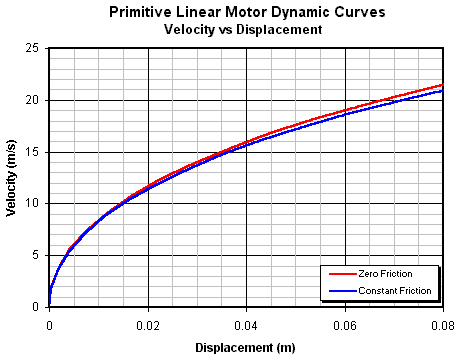
Рис. 14.10. Увеличенная кривая зависимости скорости от перемещения

Это удивительно близкие характеристики к характеристикам фактически изготовленного трехступенчатого ускорителя, тем не менее, это просто совпадение, так как есть несколько значительных различий между этой моделью и фактическим coilgun. Для примера, в coilgun сила – это функция скорости и координаты перемещения, а в представленной модели сила – это только функция скорости.

Рис. 14.11 – зависимость совокупной эффективности мотора как ускорителя снаряда. 

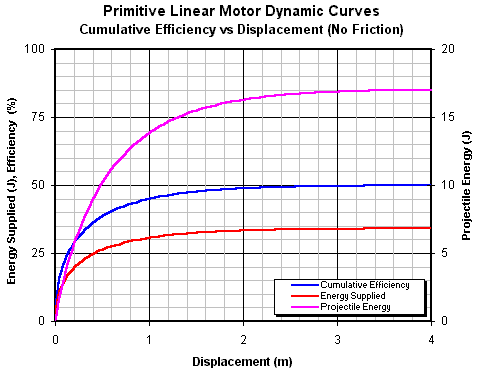
Рис. 14.11. Совокупная эффективность как функция перемещения без учета потерь трения

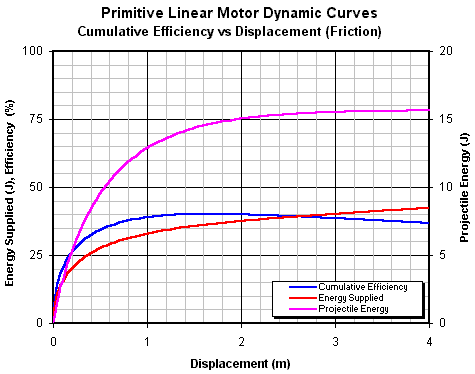
Рис. 14.11. Совокупная эффективность как функция перемещения с учетом постоянных потерь трения

Совокупная эффективность показывает фундаментальную особенность этого типа электрической машины – энергия приобретается якорем, когда он разгоняется сначала и до ‘no-load’ скорости - есть точно половина общей энергии поставленной в машину. Другими словами максимально возможная эффективность идеального (без трения) ускорителя будет 50%. Если будет трение, тогда совокупная эффективность покажет максимально эффективную точку, которая возникает из-за работы машины против трения.

В конце давайте рассмотрим влияние B на динамические характеристики скорость-перемещение, как показано на рис.14.10 и 14.11.

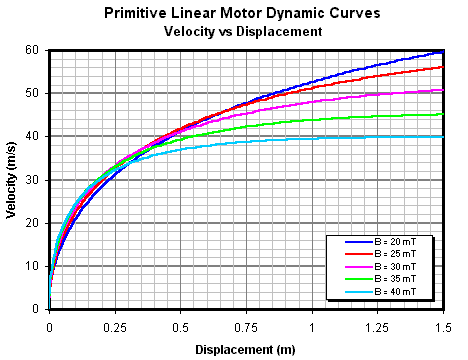
Рис. 14.11. Влияние B на градиент скорость-перемещение

 

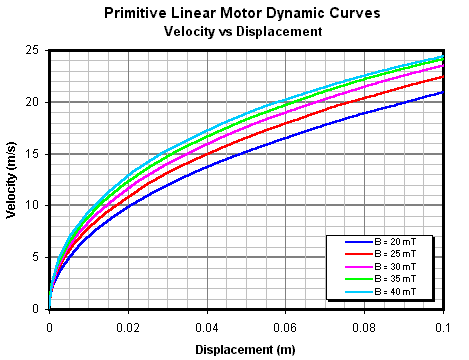
Рис. 14.12. Область небольшого перемещения, где увеличение индукции дает большую скорость

Этот набор кривых показывает интересную особенность этой модели, в которой большая индуктивность поля в начальной стадии дает большую скорость в конкретной точке, но как только скорость увеличивается, кривые, соответствующие более низкой индуктивности, догоняют эту кривую. Это объясняет следующее: Вы решили, что более сильная индукция будет давать большее начальное ускорение, тем не менее, в соответствии с тем, что будет индуцироваться большее индуцированное напряжение, ускорение будет уменьшаться более остро, позволяя, кривой для более низкой индукции догнать эту кривую.  

Итак, что мы узнали из этой модели? Я думаю важная вещь для понимания это то, что, начиная с мертвой точки, эффективность такого мотора очень низка, особенно если мотор короткий. Мгновенная эффективность увеличивается, как только снаряд набирает скорость из-за индуцированного напряжения, уменьшающего ток. Это увеличивает эффективность, потому что потеря энергии на сопротивлении (очевидно тепловые потери) уменьшается, а механическая энергия растет (см. рис 14.3, 14.4), тем не менее, так как ускорение также падает, получаем прогрессивно большее перемещение, так будет использована кривая  лучшей эффективности. (In short, a linear motor subjected to a step voltage 'forcing function' is going to be quite an inefficient machine unless it is very long.)

Эта модель примитивного мотора полезна в том, что она показывает случай типичной слабой эффективности coilgun, а именно низкого уровня движущего индуцированного напряжения. Модель упрощена и не учитывает нелинейные и индуктивные элементы практической схемы, поэтому чтобы обогатить модель нам необходимо включить эти элементы в нашу электрическую схему модели. В следующем разделе Вы узнаете основные дифференциальные уравнения для одноступенчатого coilgun. В анализе попытаемся получить уравнение, которое можно было бы решить аналитически (с помощью нескольких упрощений). Если это не удастся, буду использовать числовой алгоритм интегрирования Рунге Кутта.